Lagrange Punkte
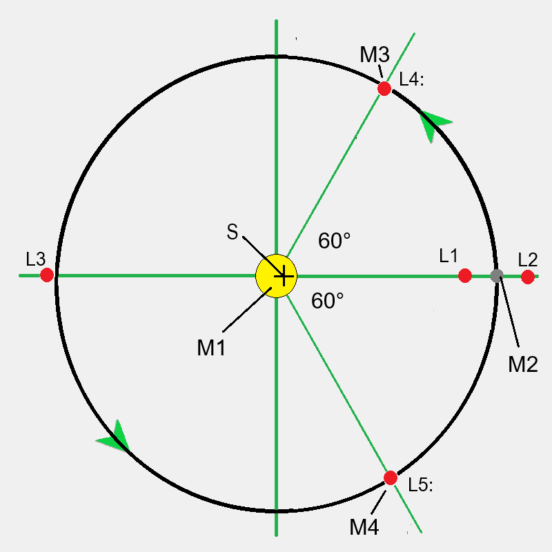
Analyse des Dreikörperproblems
(Louis de Lagrange)
- Alle Punkte L1 ... L5 liegen in einer Ebene
- L1, L2 und L3 liegen auf einer Verbindungslinie
- Berechnung des Massenverhältnis nach
Lagrange: MV = ( 25 + √ 621 ) / 2 ≈ 24,96
- L4
Masse M3 << M1 * MV und M3 << M2 * MV
M3, M2, M1 ergeben ein gleichseitiges Dreck 60°
- L5
Masse M4 << M1 * MV und M4 << M2 * MV
M4, M2, M1 ergeben ein gleichseitiges Dreck 60°
- S Systemschwerpukt M1 ... M4
In den Punkten L4 und L5 umrunden die Massen M3
oder M4 die Zentralmasse M1 ohne eigenen Antrieb.
Der Abstand von 60° zur Masse M2 bleibt dabei erhalten.
2025-07-15
Da - Durchmesser Äquator AE - 149.597.870,7 km
Dp - Durchmesser Pol Siderisches Jahr - 365,256 Tage
Dm - mittlerer Durchmesser
